
Բովանդակություն:
- Հեղինակ John Day [email protected].
- Public 2024-01-30 09:48.
- Վերջին փոփոխված 2025-01-23 14:48.

Excel- ում բոլոր 7 հիմնական տրամաբանական դարպասները պատրաստելը շատ դժվար չէ: Եթե դուք հասկանում եք Excel- ի գործառույթները, ապա այս նախագիծը բավականին պարզ կլիներ, եթե ոչ, մի անհանգստացեք, երկար ժամանակ չի տևի ընտելանալուն:
Excel- ն արդեն մի քանի տրամաբանական դարպասներ է ստեղծել մեզ համար, բայց այն չի ներառում բոլոր 7 -ը, և ամեն դեպքում մենք ինքներս ենք ցանկանում այն դարձնել:
Նախագիծը երկար չի տևում և մեկ անգամ կատարվելուց հետո կարող եք թվային թվով բազմաթիվ սխեմաներ ստեղծել Excel- ում:
Քայլ 1: Այն, ինչ ձեզ հարկավոր է
Այս նախագծի համար ձեզ շատ բան պետք չէ:
- Համակարգիչ
- Excel (խորհուրդ եմ տալիս Excel- ին, բայց նմանատիպերը նույնպես պետք է լավ լինեն)
- Հիմնական գիտելիքներ այն մասին, թե ինչպես են գործում տրամաբանական դարպասները
Քայլ 2: Ստեղծեք Excel և ձևաչափ

Սկզբից սկսեք Excel- ը (տարբերակը չպետք է մեծ նշանակություն ունենա, բայց ես օգտագործել եմ Excel 2016), այնուհետև բացեք նոր «Դատարկ աշխատանքային գիրք»:
Այնուհետև կազմեք այն ձևաչափը, որը տեսնում եք վերևի նկարում (Պատկերի ձևի պատճառով դուք պետք է սեղմեք դրա վրա `այն ճիշտ տեսնելու համար, սա վերաբերում է հետևյալ պատկերներին): Եթե չեք կարող պատճենել ձևաչափը, ապա կարդացեք հետևյալը.
B & C սյունակը դարձրեք մեկ նիշ լայնությամբ, միացրեք 1 տողը, A և B տողը:
Այնուհետև մուտքագրեք տեքստը:
Քայլ 3: Եվ դարպաս
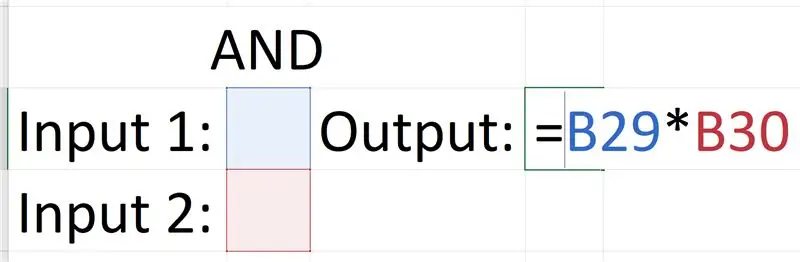
AND դարպասը ամենապարզն է, քանի որ ելքը կարող եք ստանալ ՝ մուտքերը պարզապես բազմապատկելով:
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1
Հավասարման այս արտադրանքը նույնն է, ինչ դարպասի ելքերը:
Պատճենեք բանաձևը և փորձարկեք այն ՝ տալով մուտքերը (չնայած միայն երկուական):
Հիշեք ամեն անգամ, երբ նոր դարպաս եք ստեղծում, պատճենեք դասավորությունը, որպեսզի ոչինչ չհամընկնի:
Քայլ 4 ԿԱՄ դարպաս
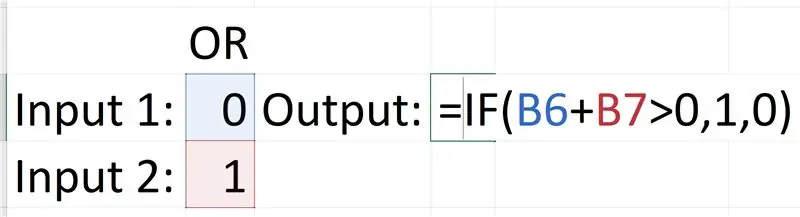
OR դարպասը ավելի բարդ է, այն պահանջում է «Եթե» հայտարարություն: «Եթե» հայտարարությունն աշխատում է այսպես. = Եթե (տրամաբանական_թեստ, [արժեքը եթե ճշմարիտ է], [արժեքը, եթե սխալ է]): Տրամաբանական թեստը, որն օգտագործում ենք, հետևյալն է. մուտքի հավաքածուն, ներառյալ 1 -ը, ավելի մեծ կլինի արժեքով (գումարային արժեք): Այսպիսով, եթե երկու մուտքերի գումարը 0 -ից մեծ է, ապա դրա դուրս գրվածը ճշմարիտ է կամ 1:
Քայլ 5: NAND դարպաս

NAND դարպասը նման է OR դարպասին, այն պահանջում է «Եթե» հայտարարություն, և դրա հետևում գտնվող տրամաբանությունը նման է: Դարպասը միայն False ելք կտա, եթե երկու մուտքերն էլ ճշմարիտ են: Այսպիսով, եթե մենք բազմապատկենք երկու մուտքերը, ապա 1 -ից փոքր ցանկացած գումար ճշմարիտ կլինի, քանի որ «Եթե» հայտարարությունը հետևյալն է ՝ մուտքագրում 1 x մուտք 2 <1, 1, 0. Եթե դա շփոթեցնող էր, ապա այս գծապատկերը կարող է օգնել.
0 x 0 = 0, 0 <1 այնքան ճշմարիտ = 1
0 x 1 = 0, 0 <1 այնքան ճշմարիտ = 1
1 x 0 = 0, 0 <1 այնքան ճշմարիտ = 1
1 x 1 = 1, 1 = 1 այնքան կեղծ = 0
Քայլ 6: NOR դարպաս

NOR դարպասը նաև օգտագործում է «Եթե» հայտարարությունը, այս դարպասի հայտարարությունն է. Քանի որ մենք երկու մուտքերն էլ միասին ենք գումարում, ցանկացած մուտքագրման հավաքածու, ներառյալ 1 -ը, երկու 0 -ից մեծ կլինի: Հետո andշմարիտ և Սխալ հայտարարությունը ցույց է տալիս, որ եթե 1 -ից փոքր գումար կա, ցույց տուր 1 -ը, հակառակ դեպքում ցույց տուր 0 -ը:
0 + 0 = 0, 0 <1 այնքան ճշմարիտ = 1
0 + 1 = 1, 1 = 1 այնքան կեղծ = 0
1 + 0 = 1, 1 = 1 այնքան կեղծ = 0
1 + 1 = 2, 2> 1 այնքան կեղծ = 0
Քայլ 7: XOR դարպաս

Սա բավականին նման է NOR դարպասին, բայց ավելի մեծ կամ փոքր խորհրդանիշ օգտագործելու փոխարեն, մենք օգտագործում ենք հավասարության նշան, քանի որ դարպասը տալիս է միայն խառը մուտքերի ճշմարիտ ելք, այնպես որ, եթե երկու մուտքերն իրար գումարենք, խառը մուտքեր միշտ կտա 1, այնպես որ մենք օգտագործում ենք հայտարարությունը. Input1 + Input2 = 1, 1, 0:
0 + 0 = 0, 0 ≠ 1 այնքան կեղծ = 0
0 + 1 = 1, 1 = 1 այնքան ճշմարիտ = 1
1 + 0 = 1, 1 = 1 այնքան ճշմարիտ = 1
1 + 1 = 2, 2 ≠ 1 այնքան կեղծ = 0
Քայլ 8: XNOR դարպաս

XNOR դարպասը բավականին պարզ է, այն հիմնականում հակառակն է XOR դարպասին, սա նշանակում է, որ տրամաբանական թեստը նույնպես հակառակն է: Այս դարպասը տալիս է True ելք միայն այն դեպքում, երբ երկու մուտքերն էլ նույն թիվն են, այլ կերպ ասած մուտքերի ցանկացած խառը հավաքածու սխալ է: XOR դարպասի տրամաբանական թեստը հետևյալն է ՝ Input1 + Input2 = 1, սակայն XNOR դարպասի տրամաբանական թեստը ՝ Input1 + Input2 ≠ 1. (≠ է Excel բանաձևերում):
0 + 0 = 0, 0 ≠ 1 այնքան ճշմարիտ = 1
0 + 1 = 1, 1 = 1 այնքան կեղծ = 0
1 + 0 = 1, 1 = 1 այնքան կեղծ = 0
1 + 1 = 2, 2 ≠ 1 այնքան ճշմարիտ = 1
Քայլ 9: ՉԻ դարպաս

NOT դարպասը պարզ դարպաս է, բայց դրա «Եթե» հայտարարությունը նույնն է, ինչ մյուսները: Այն ունի միայն մեկ մուտք, այնպես որ գուցե ցանկանաք փոխել ձեր ձևաչափը: Դարպասը պարզապես շրջում է իր մուտքը, որպեսզի բանաձևն այնքան էլ դժվար չլինի, տրամաբանական թեստը հետևյալն է.
0 = 0, ուրեմն Trueշմարիտ = 1
1 ≠ 0, ուրեմն Սխալ = 0
Քայլ 10: Թվային տրամաբանական միացում

Բոլոր տրամաբանական դարպասները ստեղծելուց հետո կարող եք դրանք օգտագործել Excel- ում տրամաբանական սխեմաներ պատրաստելու համար: Բայց ներկայիս ձևաչափը չափազանց մեծ է, այնպես որ կարող եք փորձել նոր ձևաչափը (վերևի պատկերը):
Կազմեք երկու սյունակ մեկ նիշ լայնությամբ, միացրեք վերին երկու բջիջները `ելքային ցուցադրում ստեղծելու համար, ներքևի երկու բջիջները մուտքագրում են:
Բանաձևը մուտքագրելիս մուտքագրեք ցանկալի դարպասի բանաձևը ելքային ցուցադրման վայրում:
Քայլ 11: Խնդիրների վերացում
Եթե որևէ փուլում տրամաբանական դարպասը ճիշտ չի գործում, համոզվեք, որ ձեր բանաձևը ճիշտ մուտքագրված է, և որ մուտքերը ճիշտ են կապված բանաձևի հետ:
Եթե համոզված եք, որ ամեն ինչ ճիշտ է, ապա ես, հնարավոր է, սխալվել եմ այս հրահանգը գրելիս, եթե այո, խնդրում եմ ասեք ինձ մեկնաբանություններում, որպեսզի ես շտկեմ:
Խորհուրդ ենք տալիս:
Կատարեք ձեր սեփական ջեռուցման ջերմաչափը և խնայողություն կատարեք ջեռուցման միջոցով. 53 քայլ (նկարներով)

Կատարեք ձեր սեփական ջեռուցման ջերմաչափը և խնայողություն կատարեք ջեռուցման միջոցով. Ո՞րն է նպատակը: Բարձրացրեք հարմարավետությունը ՝ տաքացնելով ձեր տունը ճիշտ այնպես, ինչպես ցանկանում եք: Խնայեցեք և նվազեցրեք ջերմոցային գազերի արտանետումները ՝ տաքացնելով ձեր տունը միայն այն ժամանակ, երբ ձեզ անհրաժեշտ է: Պահպանեք ձեր ջեռուցման վերահսկողությունը, որտեղ էլ որ լինեք: Հպարտ եղեք, որ դա արեցիք
Տրամաբանական դարպասներ ՝ օգտագործելով տրանզիստոր. 3 քայլ

Տրամաբանական դարպասներ ՝ օգտագործելով տրանզիստոր. Տրամաբանական դարպասները ցանկացած թվային համակարգի հիմնական շինանյութն են
Ապրանքների հանրագումարը, օգտագործելով տրամաբանական դարպասները. 4 քայլ
Ապրանքների հանրագումարը, որն օգտագործում է տրամաբանական դարպասները. Այս ուսանելի ծրագրում ես ձեզ ցույց կտամ, թե ինչպես ստեղծել ձեր սեփական համակարգը `օգտագործելով արտադրանքի գումարը, մի փոքր բուլյան հանրահաշվի և որոշ տրամաբանական դարպասներ: Պետք չէ ստեղծել նույն ճշգրիտ համակարգը, ինչ այս ձեռնարկում, բայց կարող եք օգտագործել
Երկակի տրամաբանական տրանզիստորային դարպասներ. 10 քայլ
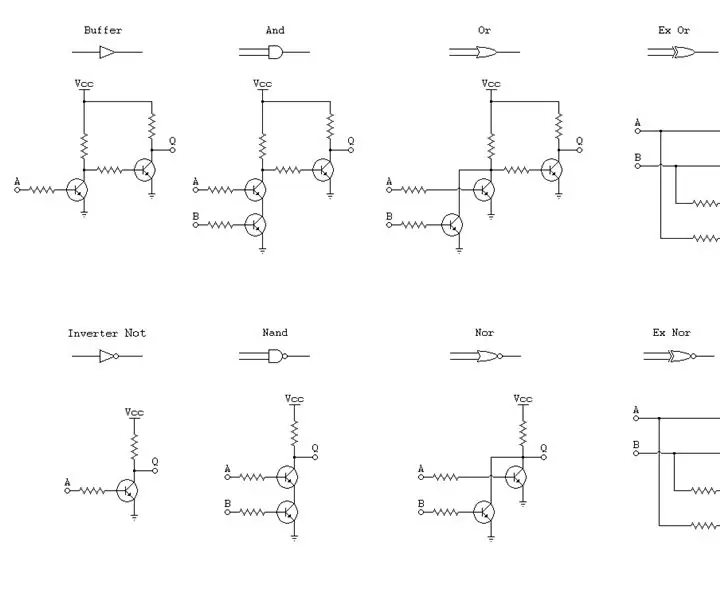
Կրկնակի տրամաբանական տրանզիստորային դարպասներ. Մարդկանց մեծ մասը, երբ կառուցում են տրանզիստորային դարպասներ. կառուցել դրանք միայն դրական տրամաբանության նկատառումով, սակայն IC- ների դարպասներն ունեն երկու տրամաբանություն ՝ դրական և բացասական տրամաբանություն: Ա
Էժան FPV անօդաչու դարպասներ. 5 քայլ

Էժան FPV անօդաչու դարպասներ. Յուրաքանչյուրի համար, ով FPV Drone (Quadcopter) Racing- ի փորձ ունի, դուք կհասկանաք Drone Gates- ի գնի վերաբերյալ վրդովմունքը: Այս դարպասները կարող են տատանվել 40 դոլարից և ավելի: Ես որոշեցի կատարելագործել oshոշուա Բարդվելի դիզայնը (https://www.youtube.com
