
Բովանդակություն:
- Հեղինակ John Day day@howwhatproduce.com.
- Public 2024-01-30 09:50.
- Վերջին փոփոխված 2025-01-23 14:48.



Այս Instructable- ում ես ձեզ ցույց կտամ, թե ինչպես կարելի է կառուցել Tic Tac Toe խաղ AI- ով ՝ օգտագործելով Arduino- ն: Դուք կարող եք կամ խաղալ Arduino- ի դեմ, կամ դիտել, որ Arduino- ն խաղում է իր դեմ:
Ես օգտագործում եմ «minimax ալգորիթմ» կոչվող ալգորիթմը, որը կարող է օգտագործվել ոչ միայն Tic Tac Toe- ի համար AI կառուցելու համար, այլև մի շարք այլ խաղերի համար, ինչպիսիք են Four in a Row, շաշկի կամ նույնիսկ շախմատ: Շախմատի նման խաղերը շատ բարդ են և պահանջում են ալգորիթմի շատ ավելի կատարելագործված տարբերակներ: Մեր Tic Tac Toe խաղի համար մենք կարող ենք օգտագործել ալգորիթմի ամենապարզ տարբերակը, որը, այնուամենայնիվ, բավականին տպավորիչ է: Իրականում AI- ն այնքան լավն է, որ անհնար է հաղթել Arduino- ին:
Խաղը հեշտ է կառուցել: Ձեզ անհրաժեշտ է ընդամենը մի քանի բաղադրիչ և այն ուրվագիծը, որը ես գրել եմ: Ավելացրի նաև ալգորիթմի ավելի մանրամասն բացատրություն, եթե ցանկանում եք հասկանալ, թե ինչպես է այն աշխատում:
Քայլ 1: Կառուցեք և խաղացեք
Tic Tac Toe խաղը կառուցելու համար ձեզ հարկավոր են հետևյալ բաղադրիչները.
- An Arduino Uno
- 9 WS2812 RGB LED
- 9 կոճակ
- որոշ մետաղալարեր և jumper մալուխներ
Լարացրեք բաղադրիչները, ինչպես ցույց է տրված Fritzing էսքիզում: Այնուհետեւ վերբեռնեք կոդը ձեր Arduino- ում:
Լռելյայն, Arduino- ն կատարում է առաջին շրջադարձը: Իրերը մի փոքր ավելի հետաքրքիր դարձնելու համար առաջին քայլը ընտրվում է պատահականության սկզբունքով: Առաջին քայլից հետո Arduino- ն օգտագործում է minimax ալգորիթմը `հնարավոր լավագույն քայլը որոշելու համար: Դուք սկսում եք նոր խաղ ՝ վերականգնելով Arduino- ն:
Arduino- ին կարող եք դիտել «մտածել» ՝ բացելով Սերիական մոնիտորը: Յուրաքանչյուր հնարավոր քայլի համար ալգորիթմը հաշվարկում է գնահատական, որը ցույց է տալիս, թե արդյոք այս քայլը կհանգեցնի Arduino- ի հաղթանակի (10 -ի արժեք) կամ կորստի (-10 -ի արժեք) կամ ոչ -ոքի (0 -ի արժեք):
Կարող եք նաև դիտել Arduino- ի խաղն իր դեմ ՝ էսքիզի հենց սկզբում չմեկնաբանելով «#define DEMO_MODE» տողը: Եթե վերբեռնում եք փոփոխված ուրվագիծը, Arduino- ն առաջին քայլը կատարում է պատահականորեն, այնուհետև օգտագործում է minimax ալգորիթմը ՝ յուրաքանչյուր հերթում յուրաքանչյուր խաղացողի համար լավագույն քայլը որոշելու համար:
Նկատի ունեցեք, որ դուք չեք կարող հաղթել Arduino- ի դեմ: Սխալվելու դեպքում յուրաքանչյուր խաղ կամ կավարտվի ոչ -ոքի կամ կպարտվի: Դա պայմանավորված է նրանով, որ ալգորիթմը միշտ ընտրում է հնարավոր լավագույն քայլը: Ինչպես երևի գիտեք, Tic Tac Toe- ի խաղը միշտ կավարտվի ոչ -ոքի, եթե երկու խաղացողներն էլ չսխալվեն: Դեմո ռեժիմում յուրաքանչյուր խաղ ավարտվում է ոչ-ոքի, քանի որ, ինչպես բոլորս գիտենք, համակարգիչները երբեք չեն սխալվում;-)
Քայլ 2. Minimax ալգորիթմ

Ալգորիթմը բաղկացած է երկու բաղադրիչից ՝ գնահատման գործառույթ և որոնման ռազմավարություն: Գնահատման գործառույթը ֆունկցիա է, որը թվային արժեք է վերագրում խորհրդի դիրքերին: Եթե դիրքը վերջնական դիրքն է (այսինքն `այն դիրքը, որտեղ կամ կապույտ խաղացողը կամ կարմիր խաղացողը հաղթել է կամ որտեղ ոչ մի խաղացող չի շահել), ապա գնահատման գործառույթը շատ պարզ է. Ենթադրենք, որ Arduino- ն խաղում է կապույտ, իսկ մարդը` կարմիր:. Եթե դիրքը կապույտ գույնի հաղթող դիրք է, ապա ֆունկցիան այդ դիրքին տալիս է 10 արժեք. եթե դա կարմիրի հաղթող դիրք է, ապա ֆունկցիան այդ դիրքին տալիս է -10 արժեք; իսկ եթե դիրքը ոչ -ոքի է, ապա գործառույթը տալիս է 0 արժեք:
Երբ հերթը հասնում է Արդուինոյին, նա ցանկանում է ընտրել քայլ, որը առավելագույնի կհասցնի գնահատման գործառույթի արժեքը, քանի որ արժեքը առավելագույնի հասցնելը նշանակում է, որ գերադասում է հաղթանակը ոչ -ոքիի փոխարեն (10 -ը մեծ է 0 -ից) և գերադասում ոչ -ոքին պարտությունից (0 -ը մեծ է -10 -ից): Նմանատիպ փաստարկով հակառակորդը ցանկանում է խաղալ այնպես, որ նա նվազագույնի հասցնի գնահատման գործառույթի արժեքը:
Ոչ վերջնական դիրքի համար ալգորիթմը հաշվարկում է գնահատման գործառույթի արժեքը ռեկուրսիվ որոնման ռազմավարությամբ: Սկսած ընթացիկ դիրքից ՝ այն փոփոխականորեն մոդելավորում է բոլոր այն քայլերը, որոնք կարող են կատարել կապույտ և կարմիր խաղացողը: Սա կարելի է պատկերացնել որպես ծառ, ինչպես գծապատկերում: Երբ այն հասնում է վերջնական դիրքի, այն սկսում է նահանջել ՝ գնահատման գործառույթի արժեքը կրելով ռեկուրսիայի ավելի ցածր մակարդակից դեպի ավելի բարձր ռեկուրսիայի մակարդակ: Այն վերագրում է գնահատման գործառույթի արժեքների առավելագույնը (եթե համապատասխան ռեկուրսիայի փուլում հերթը կապույտ խաղացողինն է) կամ նվազագույնը (եթե համապատասխան ռեկուրսիայի փուլում հերթը կարմիր խաղացողինն է) ցածր ռեկուրսիայի մակարդակից մինչև դիրքի վրա գտնվող դիրքը: ռեկուրսիայի ավելի բարձր մակարդակ: Ի վերջո, երբ ալգորիթմն ավարտեց հետքայլը և նորից հասավ ընթացիկ դիրքին, այն տևում է այդ քայլը (կամ քայլերից մեկը), որն ունի գնահատման գործառույթի առավելագույն արժեքը:
Սա կարող է մի փոքր վերացական թվալ, բայց իրականում այնքան էլ դժվար չէ: Հաշվի առեք դիագրամի վերևում ցուցադրված դիրքը: Առաջին հետադարձ քայլում կան երեք տարբեր շարժումներ, որոնք կապույտը կարող է կատարել: Կապույտը փորձում է առավելագույնի հասցնել գնահատման գործառույթի արժեքը: Կապույտը կարող է կատարել յուրաքանչյուր քայլ, կարմիրը կարող է կատարել երկու քայլ: Կարմիրը փորձում է նվազագույնի հասցնել գնահատման գործառույթի արժեքը: Մտածեք այն քայլը, որտեղ կապույտը խաղում է վերին աջ անկյունում: Եթե կարմիրը խաղում է կենտրոնական դաշտում, կարմիրը հաղթել է (-10): Եթե կարմիրը խաղա կենտրոնական ներքևի վանդակում, հաջորդ քայլում կապույտը կհաղթի (10): Այսպիսով, եթե կապույտը խաղում է վերին աջ անկյունում, կարմիրը կխաղա կենտրոնական դաշտում, քանի որ դա նվազագույնի է հասցնում գնահատման գործառույթի արժեքը: Նմանապես, եթե կապույտը խաղում է կենտրոնի ներքևի վանդակում, կարմիրը կրկին խաղալու է կենտրոնական վանդակում, քանի որ դա նվազագույնի է հասցնում գնահատման գործառույթը: Եթե, մյուս կողմից, կապույտը խաղում է կենտրոնական դաշտում, կարևոր չէ, թե որ քայլն է կատարում կարմիրը, կապույտը միշտ կհաղթի (10): Քանի որ կապույտը ցանկանում է առավելագույնի հասցնել գնահատման գործառույթը, այն կխաղա կենտրոնական դաշտում, քանի որ այդ դիրքը հանգեցնում է գնահատման գործառույթի ավելի մեծ արժեքի (10), քան մյուս երկու քայլերը (-10):
Քայլ 3: Խնդիրների վերացում և հետագա քայլեր
Եթե սեղմում եք կոճակը և լուսավորվում է կոճակին համապատասխանող մեկից այլ LED, ապա հավանաբար կամ խառնվել եք A0-A2 կամ 4-6 կապանքների լարերը, կամ LED- ները սխալ կարգով եք միացրել:
Նաև նշեք, որ ալգորիթմը պարտադիր չէ, որ միշտ ընտրի այնպիսի քայլ, որը թույլ կտա Arduino- ին հաղթել հնարավորինս արագ: Փաստորեն, ես որոշ ժամանակ անցկացրեցի ալգորիթմի կարգաբերման համար, քանի որ Arduino- ն չընտրեց մի քայլ, որը հաղթական քայլ կլիներ: Ինձ որոշ ժամանակ պահանջվեց, մինչև ես հասկացա, որ փոխարենը ընտրել է մի քայլ, որը երաշխավորում է, որ հետագայում կհաղթի մեկ քայլում: Եթե ցանկանում եք, կարող եք փորձել փոփոխել ալգորիթմը, որպեսզի այն միշտ գերադասի հաղթական քայլը ավելի ուշ շահումից:
Այս նախագծի հնարավոր երկարաձգումը կլինի ալգորիթմի օգտագործումը ՝ 4x4 կամ նույնիսկ 5x5 Tic Tac Toe- ի համար AI կառուցելու համար: Այնուամենայնիվ, նշեք, որ ալգորիթմը ուսումնասիրելու համար անհրաժեշտ դիրքերի թիվը շատ արագ աճում է: Դուք պետք է գտնեք գնահատման գործառույթը ավելի խելացի դարձնելու եղանակներ `արժեքներ սահմանելով ոչ վերջնական դիրքերում` հիմնվելով հավանականության վրա, որ դիրքը լավ կամ վատ է տվյալ խաղացողի համար: Կարող եք նաև փորձել որոնումն ավելի խելամիտ դարձնել ՝ վաղաժամ դադարեցնելով հետընթացը, եթե պարզվի, որ քայլն ավելի քիչ արժանի է այլ հետազոտությունների, քան այլընտրանքային քայլերը:
Arduino- ն, հավանաբար, ամենալավ հարթակը չէ նման ընդարձակումների համար `սահմանափակ հիշողության պատճառով: Ռեկուրսիան թույլ է տալիս կույտը աճել ծրագրի կատարման ընթացքում, և եթե կույտը չափազանց մեծանա, այն կարող է փչացնել ծրագրի հիշողությունը ՝ հանգեցնելով վթարի կամ անկանոն վարքի: Այս նախագծի համար ես ընտրեցի Arduino- ն հիմնականում այն պատճառով, որ ցանկանում էի տեսնել, թե արդյոք դա հնարավոր է անել և կրթական նպատակների համար, այլ ոչ թե այն, որ դա լավագույն ընտրությունն է այս տեսակի խնդիրների համար:
Խորհուրդ ենք տալիս:
Arduino Touch Tic Tac Toe խաղ. 6 քայլ (նկարներով)

Arduino Touch Tic Tac Toe խաղ. Հարգելի ընկերներ, բարի գալուստ Arduino- ի մեկ այլ ձեռնարկ: Այս մանրամասն ձեռնարկում մենք պատրաստվում ենք կառուցել Arduino Tic Tac Toe խաղ: Ինչպես տեսնում եք, մենք օգտագործում ենք սենսորային էկրան և խաղում ենք համակարգչի դեմ: Tic Tac Toe- ի նման պարզ խաղ է
Սխալային ալգորիթմ VHDL- ի միջոցով. 4 քայլ
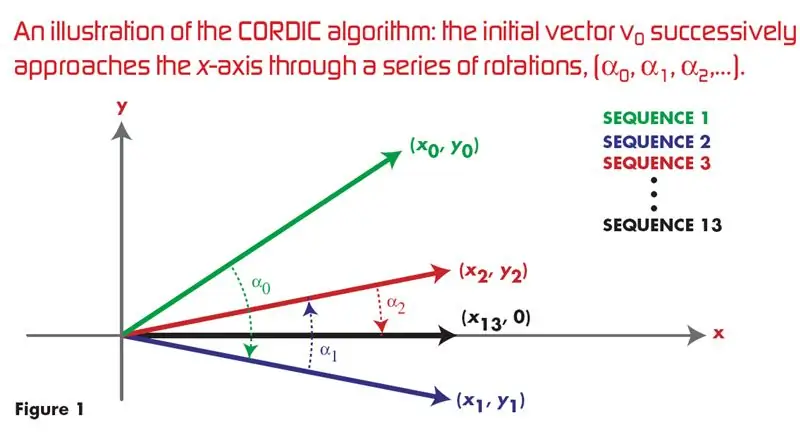
Սխալային ալգորիթմ VHDL- ի օգտագործմամբ. ## Սա Google- ում CORDIC ALGORITHM- ի VHDL իրականացման համար ամենաշատ կտտացված, ամենահայտնի հղումն է ՝ սինուս և կոսինուս ալիք առաջացնելու համար: փափուկ պատերազմի գերակայությունը
Սեղանի խաղ Արհեստական բանականություն. Minimax ալգորիթմ `8 քայլ
Սեղանի խաղ Արհեստական բանականություն. Minimax ալգորիթմ. Երբևէ մտածե՞լ եք, թե ինչպե՞ս են պատրաստված այն համակարգիչները, որոնց դեմ խաղում եք շախմատում կամ շաշկիում: Դե, մի նայեք այս Instructable- ից, որովհետև այն ցույց կտա ձեզ, թե ինչպես պատրաստել պարզ, բայց արդյունավետ արհեստական բանականություն (AI) `օգտագործելով Minimax ալգորիթմը: Օգտագործելով
Ինտերակտիվ Tic-Tac Toe խաղը կառավարվում է Arduino- ով. 6 քայլ

Arduino- ի հետ վերահսկվող ինտերակտիվ Tic-Tac Toe խաղ. Physical Tic-Tac-Toe նախագծի նպատակն է հայտնի խաղը տեղափոխել ֆիզիկական ոլորտ: Սկզբում խաղը խաղում էին երկու խաղացող թղթի վրա ՝ հերթով տեղադրելով «X» և «O» նշանները: Մեր գաղափարն էր ուսումնասիրել խաղացողների պահվածքը
3D Tic-Tac-Toe Led Cube- ի վրա. 11 քայլ

3D Tic-Tac-Toe Led Cube- ի վրա. Երբևէ ցանկացե՞լ եք տանը խաղալ Tic Tac Toe 3 չափսերով: Եթե պատասխանը այո է, ապա այս Instructable- ը ձեզ տրամադրում է բոլոր անհրաժեշտ տեղեկությունները մեկը կառուցելու համար: Խաղը կարելի է խաղալ 3x3x3 led խորանարդ: Յուրաքանչյուր կետ մեկ գույնի լեդ է, յուրաքանչյուր LE
